Por José Roberto Pacheco-Montes [1]
De manera casi dogmática siempre se ha afirmado que el inicio de todas las ciencias o áreas de estudio está anclado al desarrollo de una ciencia madre: la filosofía. Sin embargo, esto solo puede quedar de manifiesto cuando analizamos el concepto aristotélico de verdad y su vinculación con la lógica (en este caso, la silogística aristotélica). Lo anterior, debido a que comúnmente nos hemos centrado en catalogar a Aristóteles como el fundador de una concepción correspondentista de la verdad (verdad es la adecuación del intelecto con la realidad, en su versión escolástica) y no rescatamos su función predicativa. Es decir, la verdad se dice de algo y ese algo, por excelencia, solo puede ser el juicio (Cfr. Brentano, 1889/2006). Únicamente puedo decir que algo es verdadero o falso a la luz del juicio. Miremos esto detenidamente.
Aristóteles, en su Metafísica, nos dice que «[…] verdadero o falso […] es en las cosas el estar juntas o separadas, de suerte que se ajusta a la verdad el que piensa que lo separado está separado y que lo junto está junto, y yerra aquel cuyo pensamiento está en contradicción con las cosas […]» (IX, 10, 1051b 3-6). Pero ¿por qué emplea los conceptos de unión y separación? Bueno, porque si analizamos el juicio aristotélico, este está pensado como una proposición. Es decir, un juicio tiene la forma S es P o, en su defecto, S no es P; donde S representa un término sujeto y P un término predicado. Aunque, de modo más específico, tanto S como P, son clases. «Por clase nos referimos a una colección de todos los objetos que tienen una característica especificada en común» (Copi & Cohen, 2011: 213). En consecuencia, parece que Aristóteles estaba pensando que los juicios se basan en establecer relaciones entre clases y las relación pueden ser de unión o separación. Así, cuando vemos la proposición categórica tradicional: Todos los hombres son mortales, el proceso que está sucediendo es que la clase hombres está unida a la clase mortal. Algo que se puede apreciar mejor en un diagrama clásico de Venn (como el siguiente).
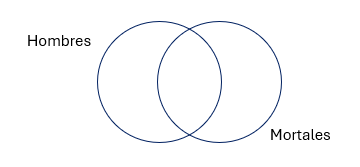
Ahí, lo que se está manifestando es que existen tres posibles relaciones en un juicio. De lado izquierdo están los hombres no mortales (si es que podemos concebir algo así), en la intersección los hombres que son mortales, y de lado derecho los mortales que no son hombres (animales, plantas o cualquier otro ser vivo). No obstante, el giro radical de esto es que Aristóteles se percata que dada una proposición categórica como la anterior podemos obtener inferencias inmediatas presuponiendo la verdad o falsedad del juicio y relacionándolas con proposiciones opuestas (oraciones que mantienen el mismo término sujeto y término predicado pero que difieren en cantidad o cualidad. Por ejemplo, si tengo la proposición: Todas las vacas son mamíferos, sus posibles oposiciones son: Ninguna vaca es mamífero, algunas vacas son mamíferos, algunas vacas no son mamíferos). Es decir, si la verdad se encuentra en las sentencias que hacemos, de algún modo podemos idear áreas de estudio, con su propia metodología, que verifiquen la veracidad del statement. Pero, de hecho, eso no es necesario para obtener nueva información, sino solo basta que analicemos que implicaciones tiene que un enunciado sea verdadero o se falso. De ahí que en las escuelas preparatorias sea común enseñarle a los estudiantes el cuadrado de oposición aristotélico.
Ahora bien, nuestro gran filósofo griego no se queda ahí, sino que se plantea: ¿qué pasa cuando concatenamos juicios? Es decir, es posible, mediante la razón, hallar nuevas verdades o falsedades presuponiendo la verdad o falsedad de un juicio, y contrastándolo con sus proposiciones categóricas opuestas. Pero, si en lugar de establecer inferencias inmediatas, buscamos hacer inferencias mediadas, ¿a qué damos lugar? Bueno, la respuesta pronta es al razonamiento deductivo del silogismo. El cual nos indica, en los Primeros Analíticos, que «el razonamiento es un enunciado en el que, sentadas ciertas cosas, se sigue necesariamente algo distinto de lo ya establecido por el <simple hecho de> darse esas cosas» (I, 24b 17-20). Así es como entonces se da inicio a la posibilidad humana de descubrir nuevas cosas y entender la posibilidad del conocer. Por tanto, ¿por qué la filosofía es la madre de todas las ciencias? Porque al hallar el lugar donde se da la verdad o falsedad de algo, se encontró que podemos verificar con nuevas ciencias si eso se da en la realidad o no. Pero, aunque nos fuera negado aquello, presuponiendo la verdad o falsedad de los juicios y uniendo unos con otros (con respectivas reglas, claro está), podemos descubrir nuevos datos y eso es la motivación de todo conocimiento científico.
[1] Masterando en Filosofía. Editor adjunto de Open Insight. Docente Prepa Tec y Universidad Anáhuac Puebla
roberto.pacheco@cisav.mx (Colocar esta cita al final del documento, por favor)
Referencias
Aristóteles. (1995). “Analíticos Primeros”. En: Tratados de Lógica (Órganon) II. Trad. Esp. De Miguel Candel Sanmartín. Madrid: Gredos.
Aristóteles. (1998). Metafísica. Trad. Esp. De Valentín García Yebra. Madrid: Gredos.
Brentano, F. (1889/2006). Sobre el concepto de verdad. Madrid: Editorial Complutense.
Copi, I., & Cohen, C. (2013). Introducción a la Lógica. Trad. Esp. Jorge Alejandro. México: Limusa.










